Animated Diffraction with Fixed Grating

Light diffraction and the use of diffraction grating is the best way to learn the wavelengths of light particles and how their varying density and angles can change the behavior of light in way of coloration. The free Animated Diffraction with Fixed Grating is a useful tool for students learning the fundamentals of light and diffraction. This template allows you to adjust various settings, such as diffraction order, ruling density, and groove spacing, to see how diffraction affect the light rays. Instead of buying a device, you can see how these subtle changes occur through the use of a single template.

Using the Animated Diffraction with Fixed Grating

This template is designed to simulate fixed grating only and is very simple to use. To download the document, click the link at the bottom of this page to get started.

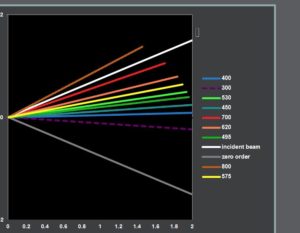
The top of the document will display the items that you can change to interact with the simulation. The first is the diffraction order (only one displayed at a time). This allows you to choose the order of light diffraction displayed in the graphic below.

The “Ruling Density” settings allow you to change the density of the beam. You will notice that after a certain point, the beam becomes monochrome.

The “Groove Spacing” option will actually change the angle of your beam. Groove spacing = d, 1000000/R. However, since the Animated Diffraction with Fixed Grating focuses on fixed grating, you will need to change the ruling density of your beam. You’re ruling density is simply seen as (Ruling density = R, lines/mm).

The last thing that you can change for this template is the incidence angle, which will change the angle at which your initial light beam will strike the simulated diffraction point and scatter your beam into multiple wavelengths.

Using the Animated Diffraction with Fixed Grating, you can see how changing the variables of light diffraction can change the wavelength of your beam, without equipment and from the comfort of your own home.

Download: animated-diffraction-with-fixed-grating-me

A special thanks to Professor T. O’Haver for his contribution.